Flash memory works fine with 4 levels per cell, but gets troublesome with 16 levels per cell due to noise.
This methods 16 levels will be as solid as 8 levels, since it can stand twice the noise.
Practically: Yes.
One extra real bit is stored in each cell.
Noise, or information theoretically: More or less 1 bit.
It depends on the shape of the noise, the errors. There is also a
small loss due to edge effects of the stored analog values.
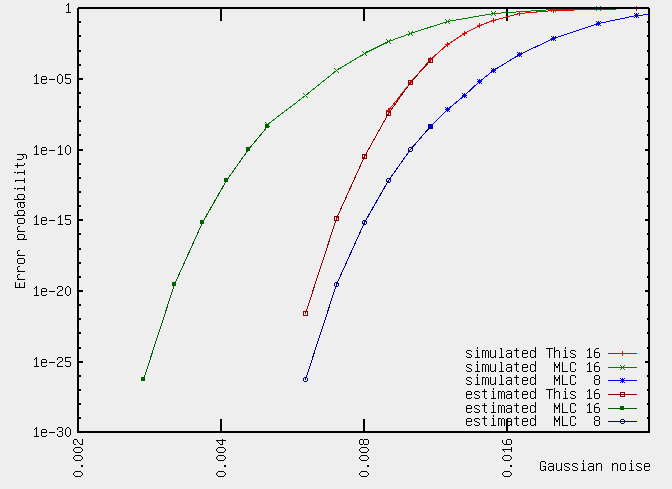
Size of minimum spike that gives error:
| 8 | Level cell: | 0.071455 |
| 16 | Levels, this system: | 0.0644530925 |
| 16 | Level cell: | 0.0333333 |
These were the results of simulating flash memory with spike errors.
As can be seen, this system has twice the noise tolerance that a 16 level cell have, while keeping 16 levels. That is, 1 bit extra.
The small difference from the 8 level spike is due to edge effects on the analog range.

As one can see, this method approaches the reliability of 8 level cells, because the red line approaches the blue at the bottom.
Encoding should be on the order of 100 times faster than noisy decoding.
If interested, contact me:
kim.oyhus@gmail.com
Snailmail address:
Kim Øyhus Odvar Solbergs vei 90, L.8013 N-0970 Oslo Norway
2009.2.14
First draft